1. For Pallas as the divinity of seven, Ficino was probably indebted either to Plutarch, De Iside et Osiride 10 ( Moralia 354F)—where the notion is attributed to the Pythagoreans; or to Macrobius, In Somnium Scipionis 1.6.11. Cf. Ficino's epitome for Plato's Republic 10 ( Opera , p. 1433): ''Attribuit Pythagorici eundem numerum [septenarium] Palladi, quia neque ex matre genita sit, neque genuerit." See Part One, Chapter 2, n. 74 above.

2. We should recall that optimates is a technical term for the Roman senatorial nobility.

3. It is associated at 544C and 545A with Crete and Sparta and usually referred to as a timocracy.

4. That is, oligarchies and democracies.

5. ab altiori ducit exordio is difficult but refers I take it to Socrates' jocose appeal to the Muses at 545D ff., just before he begins the passage on the geometric number, to address them "in a lofty tragic vein."

6. Politics 5.1316ab. Aquinas (or his continuator), who wrote on the geometric number but did not know Plato's views, complained that Aristotle's phrase was obscure because of its brevity: "Dicta Aristotelis hic obscura sunt valde propter brevitatem ipsorum" ( In Arist. Pol . lib. 5, lect. 13).

7. That is, in time itself. I take contentus here to be from contineo , not from contendo (though the latter with the dative is just possible).

8. That is, I take it, "by a particular arrangement of the stars."

9. I take the "immediate and civil faculty" to refer to Socrates' powers at this time as a political scientist. See Hankins, Plato in the Italian Renaissance 1:330-333.

10. Cicero, Epistle to Atticus 7.13.5: "Enigma . . . plane non intellexi. Est enim numero Platonis obscurius."

11. For Ficino's translation of Theon's Expositio , see Part One, Chapter 1, pp. 31-33 above.

12. The reference is either to the De Vita Pythagorica 27.130-131 (ed. Deubner; trans. Clark, p. 58), or to the In Nicomachi Arithmeticam Introductionem Liber (ed. Pistelli), pp. 82.20-83.18 ff., both of which refer, obscurely, to the Republic 8.546B, though neither passage identifies the Number. See Part One, Chapter 1, p. 35 above.

13. Again a reference to 545E.

14. For Ficino's Timaeus Commentary, see above. This remark suggests that our argumentum was written while Ficino was still working on the Timaeus Commentary (an identical reference occurs incidentally in his epitome for the ninth book of the Republic, Opera , p. 1427). It is just possible that expositio here is referring to a separate numerological treatise that Ficino was thinking of extracting from the Timaeus Commentary, just as he was to extract the third book of the De Vita from his Commentary on the Enneads 3.4.

15. Republic 8.550E ff., cf. 555C, 556C.

16. Ibid. 551C.

17. Ibid. 560BC.

18. Ibid. 564A.

15. Republic 8.550E ff., cf. 555C, 556C.

16. Ibid. 551C.

17. Ibid. 560BC.

18. Ibid. 564A.

15. Republic 8.550E ff., cf. 555C, 556C.

16. Ibid. 551C.

17. Ibid. 560BC.

18. Ibid. 564A.

15. Republic 8.550E ff., cf. 555C, 556C.

16. Ibid. 551C.

17. Ibid. 560BC.

18. Ibid. 564A.

19. Plato, Eighth Letter 354D-355A; cf. Ficino's argumentum, Opera , p. 1535.2, "improbat et extremam libertatem sive licentiam . . . mediam vero probat." See also the Republic 564A.

1. conversiones —Note Ficino's emendation in YM of the FV reading revolutiones . Proclus had claimed in his In Timaeum 4.87.16-20 (ed. Diehl) that the term periodos is ambivalent insofar as it can mean "revolution" or "the measure or duration" of a revolution. For Ficino's definitions of conversio, circulus , and ambitus and his interpretation of the argument here, see his De Numero Fatali , chapter 1.

2. ratione una cum sensu —or possibly "as long as their reason is linked to sensation, that is, while they still exist in the body." Modern translators take the clause to qualify "the wise" and thus to mean "even when their reason is combined with acute observation ( sensus )."

3. ei quod divinitus generandum est —that which has been divinely generated is the world itself, following the Timaeus 30A. Cf. Plutarch, De Animae Procreatione 13 ( Moralia 1017C); and Proclus, Platonic Theology 4.34 (ed. Saffrey and Westerink, 4:102.10-20), In Timaeum 1 (ed. Diehl, 292.6-9), and In Rempublicam 2 (ed. Kroll, 14.8-15.20, 30.6-10). See Adam, Republic , p. 204n, and Diès, Essai , p. 26.

4. circuitus quem numerus continet perfectus —This period (Greek) or circuit (Latin) is defined as the great year or the span between cataclysmic floods and conflagrations. For Ficino and the Ptolemaic tradition he inherited, it was thought to be 36,000 years. But he insists in the De Numero Fatali 17 that its span is known only to God, though God will call upon one or more of the first four perfect numbers of 6, 28, 496, and 8128, or upon a higher perfect number, or upon one of their multiples. Faber identifies conversiones and ambitus ; see Schneider, Platonis Opera Graece 3:lx, lxv.

5. humanae vero geniturae his utique in quo primo —If, however, we accept the earlier variant is as nom. sing. of is , and not as an orthographic variant for the dat. or abl. plural of hic , then the case of humanae geniturae would be dat. not gen., and we must translate "but for human begetting, this number is the first in which . . ." Cf. Proclus, Platonic Theology 4.34 (ed. Saffrey and Westerink, 4:102.21-103.2).

6. augmentationes superantes et superatae, tres distantias atque quattuor terminos accipientes —Ficino's rendering was followed by Faber and Barozzi (and we might add by Cardano and Bodin) and interpreted by them similarly. See Schneider, Platonis Opera Graece 3:vi (quoting Barozzi), lx (on Faber); and Diès, Essai , pp. 61-62 (on Faber), 79-80 (on Barozzi).

In a decision fundamental to the interpretation of this entire passage, Ficino in the De Numero Fatali 3 and 4 takes "augmentations" to be referring to the ratios between the numbers in the "numeral order" of the base, if you will, of the Timaeus 's lambda. This base consists of the two prime solids (cubes) 8 and 27 and of the two means between them, 12 and 18.

Ficino thinks of all ratios either as major ( superantes , "overcoming") or as minor ( superatae , "overcome"), the important major ones here being the double, the sesquialteral (one and a half more than one), and the sesquitertial (one and a third more than one); and the important minor ones being the half, the subsesquialteral (two-thirds), and the subsesquitertial (three-

quarters). "Overcoming" ratios "correspond" to "overcome" ratios in the sense that the ratio of the double, for instance, corresponds to that of the half.

The distances or intervals at 546B6— apostaseis (Dupuis's claim that Ficino adopted the variant apokatastaseis is incorrect and seems to be based upon a misreading of Barozzi or Bodin)—Ficino takes to be referring specifically to the three distances between the four terms in the "numeral order" (so identified and defined in De Numero Fatali 3.4-13; cf. 72-73). The major ratio for each of these is the same, namely the sesquialteral (one and a half to one, i.e., 3:2). Correspondingly, the minor is the subsesquialteral (one to one and a half, i.e., 2:3).

7. similantium et dissimilantium —The reference for these genitive plurals is grammatically ambiguous, but Ficino takes it to refer in the De Numero Fatali 4.46-55 to those classes in general of numbers that are "like" or "unlike." Square numbers are like other square numbers, cubes like other cubes. In addition unequilateral numbers can be like if their "sides" are proportional; for instance, 6 is like 24 in that 3 and 2, which are the "parts" or multiplicands of 6, share the same proportion to each other (i.e., the ratio of 3:2) as do 6 and 4, which are the parts of 24.

In the "numeral order" of 8-12-18-27, 27 and 8 are like each other as cubes, but their means 12 and 18 are unlike. However, 18 (as 6x3) and 8 (as 4x2) can also be said to be like insofar as their parts share the same ratio of 2:1; similarly 27 (as 9x3) and 12 (as 6x2) can be said to be like insofar as their parts too share the same ratio of 3:1. In the Timacus Commentary 23 ( Opera , p. 1448), Ficino analyzes the quaternary thus: 8 (2 ³ ), 12 (2 ² x3), 18 (3 ² x2), 27 (3 ³ ). Again, Faber and Barozzi followed Ficino's interpretation: see Schneider, Platonis Opera Graece 3:vi (quoting Barozzi), lx (on Faber); and Diès, Essai , p. 62 (on Faber).

Note that in actuality Plato did not refer to numbers that are "like" and "unlike" but rather to numbers that "make like" and "make unlike." Ficino's translation captures this subtlety though he interprets it to mean the same.

8. et crescentium et decrescentium —Again the reference for these genitive plurals is grammatically unclear, but in the De Numero Fatali 4.17-18, 28 ff. Ficino takes Plato to be referring to "abundant" and to "deficient" numbers respectively (for which see Part One, Chapter 2 above). Faber, Barozzi, and Cardano among others agreed; see Schneider, Platonis Opera Graece 3:vi (quoting Barozzi), lx (on Faber); and Diès, Essai , p. 62 (on Faber).

In the "numeral order" 8 is deficient, 12 abundant, 18 abundant, 27 deficient.

9. cuncta correspondencia et comparabilia invicem effecerunt —I take Ficino to mean that the augmentations or ratios among the four terms render them mutually correspondent and comparable (" prosêgora kai rhêta pros allêla " B7-C1). Thus "comparable" means expressible in the sense that 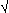49 is expressible as a whole number while 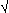50 is not. Barozzi, for instance, translates rhêta as effabilia , noting that the Latin mathematical tradition had referred to numbers such as 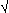49 as "rationals" and to numbers such as 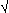50 as "surds" or "irrationals,'' improperly so, since, though they are inexpressible as whole

numbers, they are not irrational; see Schneider, Platonis Opera Graece 3:vi-vii; and Diès, Essai , p. 80 (on Barozzi).

If I am correct, then the major ratios for Ficino must render the four terms in the "numeral order" "correspondent" insofar as—in addition to the sesquialteral ratio of 3:2 which governs the adjacent numbers in the order—the ratios between the nonadjacent numbers—that is, between 27 and 8, 27 and 12, and 18 and 8—can also be expressed as it were sesquialterally—that is, as 3 ³ :2 ³ , 3 ³ :(3x2 ² ), and (3 ² x2):2 ³ respectively. Cf. Ficino's Timaeus Commentary 19 and 23 ( Opera , pp. 1446, 1448).

Moreover, the four terms are also parts of the great geometric number 1728, and if we render 1728 as (3x2 ² ) ³ , then the ratios pertaining to it and these four parts can likewise be rendered sesquialterally "correspondent" and "expressible" to each other. Thus the ratio of 1728:8 can be rendered as (3x2 ² ) ³ :2 ³ ; that of 1728:12 as (3x2 ² ) ³ :(3x2 ² ) that of 1728:18 as (3x2 ² ) ³ :(3 ² x2); and that of 1728:27 as (3x2 ² ) ³ :3 ³ .

10. Quorum —The reference is grammatically unclear, but at the end of the De Numero Fatali 12, in glossing Aristotle's comments, Ficino writes that Plato means "among the numbers" that have the same proportions—that is, ratios—as those "contained in the twelve" and in any multiple of twelve, namely 2:1, 3:2, and 4:3.

11. sexquitertia radix quinitati coniuncta —In the De Numero Fatali 3.21-26, Ficino interprets the "root" or base of the proportion of one and a third to one—for us the ratio of 4:3—as being 7. Similarly the base of the proportion of one and a half to one—the ratio of 3:2—is 5. Here the roots of the sesquitertial proportion (musically the diatesseron) and the sesquialteral (musically the diapente) are joined together, 7 with 5, to produce 12 (musically the diapason). Cf. Schneider, Platonis Opera Graece 3:vii (quoting Barozzi), lx (on Faber); and Diès, Essai , pp. 62 (on Faber), 80 (on Barozzi).

12. duas harmonias praebet ter aucta —In the De Numero Fatali 3.90-97 Ficino glosses this in effect to mean, "and having been thrice increased will supply the two harmonies that are the elements of the diapason"—that is, the diatessaron (4:3) and diapente (3:2). Cf. Schneider, Platonis Opera Graece 3:lx, lxv-lxvi (on Faber).

Though Plato is speaking of two harmonies he has not yet defined, Ficino supposes that the twelve "thrice augmented" will supply two harmonies that will replicate so to speak the two harmonies within itself. There is nothing contradictory from Ficino's viewpoint in this, since higher powers of a number replicate the proportions already contained in the first power. Hence the diapente and the diatesseron will reappear in the "third augmentation" of the twelve.

ter aucta —Note that Aristotle had substituted for " tris auxêtheis " of C2 the explanatory clause " legôn hotan ho tou diagrammatos arithmos toutou genêtai stereos ," ''meaning when the number of this figure becomes solid." Ficino slightly mistranslates this as "when the description of this number becomes solid." Perhaps he was influenced here by Donato Acciaiuoli, who, in his commentary on Aristotle's Politics of about 1472 based on Bruni's Latin transla-

tion, had glossed diagramma to mean descriptio vel figuratio —in the Venice edition of 1566 entitled In Aristotelis Libros Octo Politicorum Commentarii the gloss occurs on fol. 194v. As Fowler, Mathematics of Plato's Academy , p. 33, observes, diagramma "seems, in Plato and Aristotle, to refer ambiguously to either a geometrical figure or a proof."

In the De Numero Fatali 12.74-79, Ficino takes Aristotle to mean that the number that supplies the two aforesaid harmonies, i.e., the number 12, must then be cubed: "The beginnings of the mutations occur when the 12 by its multiplication attains first the equilateral, its plane [i.e., 144], and then reaches all the way to its solid [i.e., 1728]." Thus 12 cubed is the value of the geometric number and duly contains all the proportions originally in the 12 (cf. the De Numero Fatali 13.36, "the geometric, that is, proportional number"). Ficino must have been influenced by such commentators on the Politics as Aquinas and Acciaiuoli in supposing that by "the number of this figure" Aristotle was referring to 12 (and thus in effect making Aristotle the chief guide to his own solution!). Diès, Essai , p. 60, notes that Aquinas's commentary was often reprinted as an appendix to the Bruni translation.

In opting for 1728 Ficino was again followed with minor variations by Faber, Barozzi, and others. See Schneider, Platonis Opera Graece 3:viii (quoting Barozzi), lxii (on Faber), lxiii (Faber's rendering of Aristotle's "figure"), and lxx-lxxi (on Aquinas and Acciaiuoli); and Diès, Essai , pp. 60-61 (on Aquinas and Acciaiuoli). Faber, incidentally, seems not to have explained ter aucta .

13. unam quidem aequalem aequaliter, centum centies —In the De Numero Fatali 14, Ficino explains how the fatal geometric number (which is the sum of the two harmonies in 12 combined and then thrice increased) itself contains as it were two "harmonies" in the sense of parts or determinations (for 7 and 5 are the harmonic parts of 12 just as surely as its factors 2, 3, 4, 6 are parts). One "harmony" contains the "equally equal," that is, the squared or equilateral number of 10,000 (taking the isên isakis and hekaton tosautakis of 546C3 to be equivalents). But Ficino refers this number (which is 100 ² or 10 ⁴ ) to the myriad of fixed stars contained in the firmament (as in the De Numero Fatali 14.18-23) which is itself symbolized by 1000 (10 ³ ). One part of the geometric number is therefore 1000 (the "solid" of the universal number 10).

We might note that earlier, in the De Numero Fatali 3.82-87, he had argued that 12 contains the 10 in the ratio of 6:5; and that since 10 is the origin of all the universal numbers—100, 1000, 10,000, 1,000,000, etc.—so the universal geometric number 1728 must contain 10 and all its offspring.

For Faber and Barozzi, see Schneider, Platonis Opera Graece 3:viiii (quoting Barozzi), lx-lxi (on Faber).

14. alteram vero aequalis quidem longitudinis sed oblongiore —We might be tempted to emend the last word here to oblongiorem as Faber did, but Ficino intends a dative or ablative (and Barozzi followed him with praelongiori ) and takes it to mean "with a very oblong [result]" ( têi promêkei de [ pleurai ] C4), the dative in the Greek depending on the isos in the preceding isomêkei . Cf.

Schneider, Platonis Opera Graece 3:viiii-x, xxiii-xxiiii (quoting Barozzi, with commentary); and Diès, Essai , pp. 61, 68 (quoting Faber, who never explained this or the following phrase), 81 (on Barozzi).

The second "harmony" is therefore an oblong number with the same length as the first harmony, that is, 100, but with a shorter width. The lines immediately following are the most notoriously uninterpretable in the whole passage and determine for Ficino what the number of this shorter side is.

15. centum quidem numerorum a diametris comparabilibus quinitatis —Ficino brilliantly argues here that Plato is adverting to the number of hundreds in the second "harmony" by way of what Theon and the ancients had called the diagonal numbers. In the De Numero Fatali 5 (and 10) he gives us a summary of Theon's account of how we can arrive at rational or "comparable" diagonals for a particular succession of squares by adding or subtracting one (see Part One, Chapter 2, pp. 56-57 above). Specifically, a square with a side of 5 ( quinitatis "of the five") can be said to have not only an irrational diagonal of 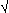50 but also a rational diagonal of 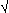49. Seven then is the width of what is "very oblong." Hence 700 as 100x7 is the second harmony in the geometric number, properly so since 7 signifies the planets (see the De Numero Fatali 14.40-41).

This leaves us still with 28, which is both the number of the Moon, her cycle, and her mansions, and also the second of the perfect numbers after 6. Six signifies, among other things, the six translunar planets. Thus the Moon as 7x4 is properly the mediator between the planets and the four sublunar elements. Presumably, for Ficino Plato did not need to single out 28 for any special definition, as Plato has declared that the geometric number is a multiple of 12 and that it contains 1000 (the eighth sphere of the firmament) and 700 (the spheres of the planets). As a fatal number it must automatically contain then the number of the most obviously fatal, because nearest, of the planets, the Moon.

We should recall that there are seven terms in the lambda and that each of the two progressions in it—1-2-4-8 and 1-3-9-27—has four terms plus three intervals. The number 7 says Theon in his Expositio 2:46 is endowed with a marvelous property ( thaumaston echei dunamin ) since alone in the decade it has no multiple or divisor. Cf. the famous salutation in the Aeneid 1:94, "O terque quaterque beati"; and Plutarch's declaration in De E apud Delphos 17 ( Moralia 391F) that 7 is consecrated to Apollo.

16. singulis ingentibus uno —The individual diagonals "each requiring one" ( deomenôn henos hekastôn C5). This "requiring one" is the key element in the theory of diagonals Ficino outlines in his De Numero Fatali 5. Cf. Theon, Expositio 1.31.

17. duobus vero qui non sunt comparabiles —The most difficult of the cruces in this crux-laden passage. Ficino translates the Greek quite literally, but the only clue to his interpretation occurs in the De Numero Fatali 5.37-39 where he writes that the diagonals and their accompanying laterals "need the 1 as their equalizer," the "incomparables singly, the comparables together." Here I take it he is interpreting Plato to be saying, not that the incomparables need 2, since he has just said that they need 1, but rather that

you must add or subtract 1 either to the power of the diagonal by itself or to the sum of the powers of the two sides together. Thus for a rational diagonal of 7 we would have either 7 ² =5 ² +5 ² -1 or 7 ² +1=5 ² +5 ² ; and for one of 3 we would have either 3 ² =2 ² +2 ² +1 or 3 ² -1=2 ² +2 ² .

Clearly, this is a contorted interpretation of a baffling clause, which had been satisfactorily explained only by Proclus (or his source), though Proclus's solution (which presupposes a different value anyway for the geometric number) was completely unknown to Ficino as we have seen; see Diès, Essai , pp. 28-36.

Faber, by contrast, takes the duoin of C5 to be referring to the diametrôn of C4 and hence to mean "[from] the two diagonals that are indeed inexpressible," and not as Ficino and other modern interpreters to be referring to the deomenôn of C5 and hence to mean "requiring two." Diagonals for him are "inexpressible" when they have no "expressible" ratio to their sides: thus the square with a rational diagonal of 3 and sides of 2 has the ''expressible" sesquialteral ratio, whereas the square with a rational diagonal of 7 and sides of 5 has the "inexpressible" ratio of 7:5. For Faber, Plato is referring to two "diagonals," because every square has two diagonals; see Schneider, Platonis Opera Graece 3:lxii, and Diès, Essai , p. 63.

Barozzi arrives at an even more complicated explanation because he takes Plato's deployment of the idiom arithmoi apo at 546C4-5 (" hekaton men arithmôn apo diametrôn rhêtôn pempados ") to signify the squaring of a number—probably correctly—and thus that Plato intended us to arrive at the number of the width by way, not of the two irrational diagonals themselves, but of their powers or squares; see Schneider, Platonis Opera Graece 3:xi-xii, and more especially Dupuis, Nombre , p. 42.

18. Centum vero cuborum trinitatis ipsius —Again Ficino follows Aristotle's gloss (in the Politics 1316a6-7) in interpreting this to refer to the 100 raised to its third power, i.e., to a million, "of the three" being a formula for Ficino signifying cubing. For him Plato's intention here was to present the power of the 100 (itself the power of the universal number 10) under three guises: as the origin of the higher equilateral power of the 10,000 (the number of the fixed stars in the 1000 of the firmament); as the length to be multiplied by the number 7 (7 being both a diagonal number and the number of the planets); and as the origin of the solid or cube power of 1,000,000.

Underlying Ficino's analysis is the notion that the 100 appears here in the guise first of a plane, then of a diagonal (i.e., that which defines this plane as a square surface), and then of a cube (the plane raised to a solid).

Some commentators have taken the third mention of the 100, "the hundred of the cubes of the three," to mean 100 times the sum of the cubes of the three numbers (i.e., 3, 4, 5) in the perfect Pythagorean triangle—that is, 100x216. Others have maintained that Plato means 100 times the cube of 3—that is, 100x27. Ficino was also convinced of the presence in the passage of the Pythagorean triangle, but only in the general sense that the sum of its three numbers is 12 and that it can be thought of as containing the two critical ratios of 4:3 and 3:2.

For Faber's and Barozzi's differing position, see Schneider, Platonis Opera

Graece 3:x-xii, lxi-lxii; and Diès, Essai , pp. 62-63, 68-69 (on Faber). Faber regarded 100x100 as the fatal if not as the geometric number, and 1,000,000 as the cube "of the three" in the sequence of 100, 1,000, 1,000,000, and 100 as the cube "of the three" in the sequence of 1, 10, 100.

19. That is, the geometric number is not a perfect number. But the geometric number does contain the first two perfect numbers nonetheless: the 6 (as the origin of 12) and the 28 (as the terminal number of 1728).

20. Notice the recurring play on the "opportune" moments given us by "opportunity" as contrasted to less happy results occasioned by "occasion."

21. That is, possessed of a benign and fortunate disposition and intelligence.

1. The Greek kuklos is singular. In transliterating it Ficino uses it as an accusative plural.

2. The peritropê is the perfect circular motion of the substance, of the kuklos , of a heavenly sphere, and therefore of all the fixed stars in the eighth sphere of the firmament.

3. The periphora is the irregular course of a planet as contrasted with the regular peritropê of a sphere.

4. As irregularly regular, the planetary revolutions serve as the medium by which, in their perfect regularity, the spherical conversions selectively work upon the imperfect and irregular course of things earthly by way of their individual properties and the state of their preparation. Note Ficino's insistence on what elsewhere he refers to Neoplatonically as the ''series" or "chains" of accord that bind the universe; see, for instance, his De Vita 3.14.

5. Thus things earthly at "the center" are governed by spherical as well as earthly measures, by conversions as well as revolutions, though we do not know which particular stellar conversions or how many of them are involved in measuring the life cycle of any one species or individual. For a list of the major stars known to Ficino, see his De Vita 3.8.1-41 (ed. Kaske and Clark), where it is attributed to Hermes Trismegistus.

6. Thus "fate" means the combined measures of stellar conversions and planetary revolutions. All sublunar life is the result of its interaction with natural properties in the species and in the individual, provided they are "prepared" or in "accord." The complexity of fate's relationship with nature is thus unfathomable except to God or to someone inspired by Him.

7. Ingenium is an important concept in this treatise; see Part One, Chapter 3, pp. 88-89, 100 above. It is to be identified with our intellectual capacities insofar as they are governed by, are in accord with, our temperament and disposition. It is not clear whether for Ficino such a corporate entity as a family, a state, or a nation can also have an ingenium; and if so, what its relationship would be to the notion of a presiding genius or daemon. The ramifications are legion. Contrast De Vita 3.23.10-20 and passim (including the chapter heading) with 3.24.18-21 (ed. Kaske and Clark).

8. Ficino returns to the role of the perfect number(s) in his last chapter and to the notion that God has destined certain divine or daemonic intellects to have knowledge of, and to preside over, the terms of the durations measured by such a number or such numbers. For their definition, cf. Theon, Expositio 1.32 (ed. Hiller, pp. 45.9-46.3). Plutarch's famous essay De Defectu Oraculorum argues that great daemons also preside over measurable, if multigenerational, durations.

1. The "numberless" Ficino identifies as a Platonic term for myriads, that is, numbers between 10,000 and a million. What he has in mind here is probably 36,000 (i.e., 6 ² x1000), for this is the value he accepts for the great year in his epitome for the Republic 10, and in his argumentum for the Laws 6 ( Opera , pp. 1431, 1505); see too his Timaeus Commentary, summa 20 ( Opera , p. 1468.2).

2. The parts are the factors of the perfect number and they measure the span of a "form," presumably in the Aristotelian sense of what is united with matter to make an entity. Ficino has in mind the appointed span of an individual person's life or that of an entity like a state, a span that has been allowed to run its full and perfect course. In chapter 3 below, however, he will declare that 12 is the number that governs "the universal world form, the human form, and the form of the state."

3. Cf. Ficino's Platonic Theology 17.2 (ed. Marcel, 3:155) and De Vita 2.20.1-21 (ed. Kaske and Clark). He was familiar with the idea from a number of ancient sources, e.g., Theon, Expositio 2.46 (ed. Hiller, p. 104.1-12), and Proclus, In Alcibiadem 196 (ed. Westerink, pp. 90-91).

4. Ficino is now going to mention in passing the particular roles played in measuring durations by 6, 8, and 12 and then by various kinds of numbers (unequilateral, equilateral, solid, diagonal).

5. See chapter 4 below. For the notion of deficiency, i.e., that the sum of a number's factors (or divisors or aliquot parts) is less than itself, cf. Theon, Expositio 1.32 (ed. Hiller, p. 46.9-14). Eight is solid, however, in that it is the cube of 2. As such it is the first of the solid numbers.

6. Again see chapter 4 below. An abundant number is greater than the sum of its factors; cf. Theon, Expositio 1.32 (ed. Hiller, p. 46.4-8). Twelve is the first of such numbers.

7. The unequilateral "long" numbers are the sums in the regular series of even numbers, beginning with 2: 2+4=6, 2+4+6=12, 2+4+6+8=20, 2+4+ 6+8+10=30, and so on; and as sums they are always even and therefore female (cf. chapter 6 below). As multiples, however, the "longs" are the products of adjacent and therefore odd and even numbers—2x3, 3x4, 4x5, 5x6, and so on—while unequilateral ''oblong" numbers are the products of numbers differing by more than 1. The latter are of little or no interest to Ficino here or to the arithmological tradition in general. Cf. Theon, Expositio 1.13 (on unequilaterals), 17 (on oblongs) (ed. Hiller, pp. 26.21-27.22, 30.8-31.8).

8. Equilateral numbers are the sums in the regular series of odd numbers, beginning with 1: 1+3=4, 1+3+5=9, 1+3+5+7=16, 1+3+5+7+9=25, and so on; and they alternate between being even and being odd. As products, however, they are also the squares of the regular series of odd and even numbers. Cf. Theon, Expositio 1.15 (on equilaterals), 20 (on their alternation) (ed. Hiller, pp. 28.3-15, 34.1-6).

9. A solid number is the product of three numbers and can be of four kinds: a cube, altar, plinth, or beam. Cf. Theon, Expositio 1.7 (the definition), 29 (the four kinds) (ed. Hiller, pp. 24.25-25.3, 41.8-42.2). But Ficino is exclusively interested here in cubes.

10. That is, in the commentary on (or epitome for) the section in the Republic 9 at 587C-588A on the number 729. Ficino's epitome for this ninth book was written, however, prior to 1484, and merely states, "Inter haec casu quodam nescio quid interserit mathematicum, cuius declarationem ex commentariis in Timaeum accipies opportunius" ( Opera , p. 1427). His remark here refers therefore to comments he will make towards the end of chapter 3 below.

11. Ficino is referring to the powers of rational diagonals in the series of squares he will outline in chapter 5 below.

Note that throughout I have rendered diameter as a "diagonal" since Ficino is dealing with a square's diagonal, and not with a diameter ( diametros in Greek can mean both); obviously such a diagonal is the same as the hypotenuse of the isosceles right-angled triangle that constitutes one half of the said square. A numerus diametralis correspondingly is a "diagonal number" (often thought of in terms of its power, that is, as squared).

1. Namely, at Republic 8.546B. In Ficino's view, as his subsequent comments testify, this passage is referring to the Timaeus 's lambda with its base of 8-12-18-27; cf. Theon, Expositio 2.38 (ed. Hiller, pp. 94.11-96.8).

2. Timaeus 35B-36B, 43D. Plato had argued at 31B ff. and 36A ff. that to define the numerical relationship we always need between solid numbers two means, but between square numbers just one mean. Ficino had already dealt with the problem in his Timaeus Commentary 19 and 23 ( Opera , pp. 1446.1, 1448.1).

3. See Part One, Chapter 2, nn. 7, 8 above. Cf. Theon, Expositio 1.16 (ed. Hiller, pp. 28.16-30.7) on the fact that equilaterals embrace unequilaterals as proportional means but not the reverse. Twelve is a plane insofar as it is the product of 3x4; it is an unequilateral as a member of the unequilateral series; and it is a mean between 16 and 9 in that 16:12 and 12:9 are both in the ratio of 4:3.

4. The logic of the argument requires that the means between the solids 8 and 27 cannot be the two equilateral planes referred to here—namely 9 and 16—but rather 12 and 18 as already stated (though 18 is not part of the unequilateral series). I have emended the text accordingly by omitting plana .

5. That is, the interval of the fifth; cf. Theon, Expositio 2.13, 37 (ed. Hiller, pp. 62.1-63.24, 93.17-25).

6. That is, the interval of the fourth; cf. Theon, ibid.

7. That is, the full octave that includes the fifth and the fourth; cf. Plato, Timaeus 36AB and Theon, ibid.

8. Ficino uses the term compositio to mean addition. Thus 5—the "root" of the ratio 3:2—when "compounded" with 7—the "root" of the ratio 4:3—makes 12.

9. Commixtio means multiplication; and the "parts" are the parts of the "root." In these two cases the parts are 4, 3, and 2; and 4x3, 2(3x2), and 3(2x2) all equal 12, as Ficino goes on to explain.

10. The refusal to accept 1 or 2 as numbers in the strict sense was traditional; cf. Theon, Expositio 2.42 (ed. Hiller, p. 100.13-17). Hence 3 became the first number as the first determined "multitude" and 4 the first square, since it contains the first even and the first odd number; cf. Ficino's Timaeus Commentary 20 ( Opera , p. 1446.2). At 2.44 (ed. Hiller, p. 102.3) Theon had declared that 1 is not a number, and at 2.41-42 (ed. Hiller, p. 100.9-17) he had implied that 2 is not a "determined" number.

11. Phaedo 110B-111C. Cf. Ficino's epitome ( argumentum )in his Platonis Opera Omnia (1491), fol. 175v (sig. y3v) (i.e., Opera , p. 1394): "Quod autem terrae sublimis faciem in duodecim dividit plagas inde provenit quia duodecim congruit zodiaci signis, duodecim spherarum regitur animabus, et duodecima est mundi sphera, atque veluti totius fundamentum dodecaedram illam sibi usurpati [ Op . usurpati] figuram quam Timaeus attribuit mundo."

12. Critias 109B ff., 113BC—the gods had the earth apportioned among them? There is no mention of 12 here, and although there are twelve Olympians, Critias explicitly says that Athena and Hephaestus, since they shared a love of wisdom and artistry, shared one allotment, namely Attica! Ficino's Critias epitome in his Opera , pp. 1485-1488, nowhere refers to the twelve regions, though it does refer to the flood; and he probably interpreted the allusion in the light of the Phaedo 110B ff. to which he has just referred.

Interestingly, the Critias epitome refers to "Origenes" using the Republic 8 [i.e., at 546A4 ff.] to point out that "certain celestial circuits are the causes of fertility and sterility both of bodies and of souls" (p. 1487). Ficino's acknowledged source is Proclus's In Timaeum 1:162.29-30 (ed. Diehl; trans. Festugière, 1:216). This should alert us to the importance for Ficino of adjacent sections of Proclus's commentary, sections glossing the two lemmata at Timaeus 24C5-6 (" Eklexamenê ton topon " and '' eukrasian tôn hôrôn ") and devoted to the themes of Athena's "allotment" or "choosing" of Attica and of what makes a certain place propitious.

13. Laws 5.745B-E, 746D, 6.771BC. Cf. Ficino's epitomes in his Opera , pp. 1502, 1504-1505, 1522 (to the opening of book 12). For 12 as the symbol of "perfect procession," see Proclus's Platonic Theology 6.18, 19 (ed. Portus, pp. 394-400).

14. Phaedrus 246E-247E. Cf. Ficino's Phaedrus Commentary 11 (ed. Allen, pp. 124-127).

15. Timaeus 55C4-6—an allusion to the dodecahedron. See also the Epinomis 981BC and cf. Ficino's Timaeus Commentary 44 [misnumbered 41] ( Opera , p. 1464.1 verso). I quote from the latter as it appears in the Platonis Opera Omnia of 1491, fol. 251r-v (sig. H3r-v): "Denique dodecaedram figuram mundo, ut dicebam, accommodavit, quoniam siderum formae duodecim suspiciuntur in zodiaco quorum quaelibet in partes triginta secatur. Similiter in figura dodecaedra intueri licet pentagonos duodecim singillatim in triangulos aequilateros quinque divisos ita ut unusquisque rursum ex triangulis sex [ Op. om. ] scalenis conficiatur et in omni mole dodecaedra trecentisexaginta reperiantur trianguli quot [ Op. quod] etiam zodiaco portiones existunt." Cf. Plutarch, Platonicae Quaestiones 5.1 ( Moralia 1003CD).

We might note that the extant portions of Calcidius's In Timaeum only go up as far as 53C and those of Proclus's In Timaeum only as far as 44D2 (and

in the MS which Ficino used, the Riccardiana's gr. 24, only as far as 35B2). Neither commentary therefore was directly relevant. Incidentally, Proclus's In Timaeum —an important resource for Ficino—contains in its entirety just seven inconsequential allusions to the Republic 8.546A1-D3 (and in the Riccardiana's partial MS just three!); see the index testimoniorum in Boter's Textual Tradition , pp. 345-346.

Moreover, Ficino cannot have read the thirteenth treatise of Proclus's In Rempublicam 13 (ed. Kroll, 2:45.6-46.18; trans. Festugière, 3:152-153), which deals with the dodecahedron, since he worked from a MS which only contained the first twelve treatises (see Part One, Chapter 1, n. 88 above).

16. Platonic Theology 4.1 (ed. Marcel 1:153-155). See respectively nn. 13 and 15 above for the references to Ficino's Laws epitomes and his Timaeus Commentary (though he treats no further of the 12 there and he may be thinking rather of passages in his epitome for book 10 of the Republic [ Opera , pp. 1431, 1433]).

17. That is, the forms of the world body, of the human body, and of the body politic; cf. chapter 2, n. 2, above. The reference here to the human body is to the zodiacal man, i.e., to the traditional theory that goes back to Ptolemy and beyond that the body can be divided into twelve parts presided over by the signs of the zodiac. See my "Homo ad zodiacum."

18. See chapter 4, par. iv below.

19. For circular numbers, cf. Theon, Expositio 1.24 (ed. Hiller, pp. 38.16-39.9), and Ficino's Timaeus Commentary 17 ( Opera , pp. 1444.4-1445).

20. For the Sun, Venus, Jupiter, and the Moon as the "fountains" of life, see chapters 12 par. iv, 14 par. iii, 16 par. ii, and 17 par. iii below. Cf. Plato, Cratylus 396AB: "For there is none who is more the author of life for us and for all than Zeus the lord and king of all. Wherefore we are right in calling him Zena and Dia, which are one name, although divided, meaning the god through whom all creatures always have life ( di' hon zên aei pasi tois zôsin huparchei B1-2)." This was a passage to which Ficino often referred, e.g., in his Philebus Commentary 1.26 (ed. Allen, pp. 246-247).

21. That is, from a Ptolemaic perspective, their orbits around the earth. Cicero, for instance, in his De Natura Deorum 2.20.52-53, gives the received orbital times of the planets as follows (the actual sidereal periods follow in parentheses): Saturn about 30 years (29 years 168 days), Jupiter 12 years (11 years 314.1 days), Mars 2 years minus 6 days (1 year 321.9 days), Venus 1 year (224.7 days), and Mercury about 1 year (87.97 days). Cf. Theon, Expositio 3.12.

22. This is difficult. I take it that motu medio means "in her motion across or to the middle of heaven" or "midway through her motion." The Moon traverses 28 mansions in all (28 being the second perfect number), and each mansion consists of 12 degrees (actually of 12.857142 degrees). She traverses one a day. The mansions are positioned among both the 12 zodiacal signs and the 12 arcs of the divided ecliptic, the 12 plagae or mundane houses, though these are not coterminous. Since each sign and each plaga are divided into 30 degrees, she variously traverses each in two and a third days.

We might note that in the De Vita 3.4.68-69 (ed. Kaske and Clark) Ficino had referred to the theory that the Moon is in conjunction with, in opposition to, or in an aspect with, other planets if it is within 12 degrees on either side of the various requisite positions, a margin of error called the "orb."

23. An open reference. Twelve is significant in the Scriptures as the number of the tribes of Israel and of Christ's disciples, and in the Book of Revelation as the number of the gates of the New Jerusalem (21:12-14), the number of stars in the crown of the woman clothed with the sun (12:1), the manner of fruits born by the tree of life (22:2), and the number of the "sealed"—in that 144,000 is the total number of the twelve tribes, each of 12,000 (7:4 ff.).

24. Cf. Ficino's Phaedrus Commentary, summa 25 (ed. Allen, p. 169); also the Theologumena 80 (ed. de Falco), and Theon, Expositio 2.37, 39, 49 (ed. Hiller, pp. 93.17-25, 99.17-23, 106.7-10)—on the decad as the sum of the tetraktys and the number to which all others are "brought back."

25. At 587C-E ff. Ficino's epitome ( Opera , pp. 1426-1427) contains nothing of relevance.

26. That is, 12 contains the product of 2x5. It is that product added to its two-tenths (i.e., its fifth).

27. That is, diapente and diatesseron, the "consonances" of the fifth and the fourth respectively; see nn. 5 and 6 above.

28. The readings in both Y and Z are clearly wrong, and the passage is missing in M.

29. The average length of a lunar sidereal circuit is 27 days, 7 hours, and 43 mins., while that of a lunar synodic period (the interval between one new moon and the next) is 29 days, 12 hours, and 44 mins. Ficino is approximating the difference between the two periods.

30. This is presumably again a reference to 587E ff., which adduces 729 as a "true number . . . pertinent to the lives of men if days and nights and months and years pertain to them" (588A).

31. Cf. n. 22 above.

32. The seven planets bestow two "perfections" upon us, the six superior planets, the first perfection, and the Moon in her twenty-eight mansions, the second, 6 and 28 being the first two perfect numbers.

33. That is, Plato is going to present us with two fatal numbers that are cubes: with 729 as the cube of 9, and with 1728 as the cube of 12. Cubing is taken to be the "highest" power, because geometrically it creates three-dimensionality. Sublunar nature is governed by cyclical movement, and this is symbolized by the raising of a number to its third power and the reduction of that power to its cube root.

1. At 546B5: " auxêseis dunamenai te kai dunasteuomenai ."

2. That is, 1:2 reverses 2:1, 1:3 reverses 3:1, and so on.

3. Cf. Theon, Expositio 2:31 (ed. Hiller, p. 82.12-21).

4. partientes vero minuunt quasi continuum is difficult. Continuum might mean more literally the smaller number "joined to" a larger and dividing it. But the point is that the proportions—that is, quotients—increasingly diminish, because, even though the dividends increase, the divisors increase too.

5. Cf. Theon, Expositio 1.32 (ed. Hiller, p. 45.19-22).

6. Cf. Theon, Expositio 1.32 (ed. Hiller, p. 46.9-12).

7. Cf. Theon, Expositio 1.32 (ed. Hiller, p. 46.4-8).

8. The equilaterals 9 and 16 are the result of the addition series of odds, 1+3+5+7, etc., which produces a succession of sums which as products are squares. Since 16 is also the sum of 12's aliquot parts, it means that 12, itself an unequilateral, shares in 16, an equilateral.

9. For 6 as the first spousal number—that is, the first product of a union between a male (odd) and a female (even) number—cf. Theon, Expositio 2.45 (ed. Hiller, p. 102.4-6); also the Theologumena 43, and Iamblichus, In Nicomachi Arith. Introd. (ed. Pistelli, p. 34.19 ff.).

10. That is, for numbers to be spousal they must be adjacent; 3x6 or 9x2 are not spousals and 18 is not therefore a spousal number. From the perspective of addition, spousals are the "long" unequilaterals. Cf. the Theologumena 43.

11. At 546B6-7: "making similar" (" homoiountôn "), "making dissimilar" ('' anomoiountôn "). Cf. Theon, Expositio 1.22 (ed. Hiller, pp. 36.12-37.6).

12. Twenty-four is an "oblong" unequilateral, being the product of 6x4. Cf. Theon, Expositio 1.22 (ed. Hiller, p. 36.15-20), who takes 6 as 3x2 and 24 as 6x4 and establishes their proportionality by way of the formula 6:3 = 4:2.

1. Cf. Theon, Expositio 1.3, 4, 7, 19, 23, 31 (ed. Hiller, pp. 18.6, 19.21, 24.23, 33.5-7, 37.17-19, 43.4-8, 10-11).

2. Note that Ficino is not thinking in terms of an isosceles right triangle.

3. Cf. Theon, Expositio 1.31 (ed. Hiller, pp. 42.10-45.8).

4. Again cf. Theon, Expositio 1.31 (ed. Hiller, p. 44.3-8).

5. Again cf. Theon, Expositio 1.31 (ed. Hiller, p. 44.9-12).

6. Compensatio in the sense of adaequatio —the reestablishment of equality or balance.

7. Again cf. Theon, Expositio 1.31 (ed. Hiller, pp. 44.12-45.8).

8. By "incommensurables" and "commensurables" Ficino means here the diagonals and the sides. The commensurable sides together need the 1 as "equalizer" in the sense that 1 has to be added to, or subtracted from, the sum of their squares in order for that sum to equal the square of their "rational" diagonal—as in 5 ² +5 ² -1=49 (where 49=7 ² )—though the actual diagonal is 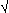50 and therefore irrational in the sense of "incommensurable." Put another way, 1 must be added to or subtracted from the square of the "rational" diagonal in order for it to equal the sum of the squares of the two commensurable sides—as in 7 ² +1=50 (where 50=5 ² +5 ² ). The one diagonal "singly"

needs the equalizing 1, whereas the two sides need it "together." Ficino thus tries to account for the famous crux at 546C5.

9. A reference to his treatment of commensuratio (i.e., of rational numbers) in chapter 10, par. iv below.

10. That is, the proportion of sesquialter , of 1 1/2 to 1—in music the harmony or "consonance" of the fifth called diapente.

11. At 546C5: " pempados ."

12. At 546C6: " triados ."

13. He may be referring here specifically to the perfect cube of the 9 tripled, namely to 729, the number introduced in the ninth book of the Republic at 587E; or more generally to any solid constituted entirely or even partially from 9 or from any of its multiples.

1. Cf. Theon, Expositio 1.7 (ed. Hiller, pp. 24.16-25.4).

2. Obviously we can have equilateral planes such as 2x2 and unequilateral planes that are long such as 2x3 or oblong such as 2x6. Ficino cannot ignore the oblongs given the oblongiori/e of Plato's text.

3. Of course, certain numbers are both long and oblong: 12 for instance is long as 3x4 but oblong as 6x2, as Theon observes in his Expositio 1.17 (ed. Hiller, p. 30.18-23).

4. Again as Theon observes in his Expositio 1.17 (ed. Hiller, pp. 30.23-31.2), some numbers are only oblongs; 40, for instance, is triply so as 20x2, as 10x4, and as 8x5.

5. That is, multiplication is seen metaphorically as a begetting between two numbers that "commix"; if such numbers are adjacent (i.e., long), they are "spousals." Cf. chapters 3, n. 9 (on commixtio ), and 4, n. 10 (on spousals) above.

6. Ficino begins with a consideration of the two number series created by the addition of odd numbers and then by that of even, postponing until the next chapter his consideration of a third, the so-called trigon, series, which is created by the addition of odd and even numbers together. He does so because he needs to establish definitions first for equilateral and then for unequilateral numbers. Theon had adopted the same order in his Expositio 1.13-19 (ed. Hiller, pp. 26.21-33.18).

7. Cf. Theon, Expositio 1.15 (ed. Hiller, p. 28.3-15).

8. The resulting series—1, 4, 9, 16, 25, 36, 49, etc.—contains of course alternating odd numbers, but the even numbers in it are themselves the result of the addition of two odd numbers (as 4 is constituted from 1+3 and 16 from 9+7 and 36 from 25+11). Viewed as multiples, the series is identical with the series of the square numbers. Hence a number such as 16 can be seen as the result either of multiplication (4x4) or of "equilateral" addition (9+7), the latter being primary for Ficino and the Pythagorean tradition.

9. That is, whereas 1 is the leader of all odd numbers and of some even numbers (i.e., of those in the series produced by equilateral addition as just

described), 2 is the leader of the even numbers produced by unequilateral addition (which Ficino is about to describe).

10. Cf. Theon, Expositio 1.5 (ed. Hiller, p. 22.13-16).

11. On the primary triangles, see Timaeus 57D, 58D, 73B, 89C, and, for the notion of a triangle's perfect form, 53C ff. On triangular numbers, cf. Theon, Expositio 1.19 (ed. Hiller, pp. 31.13-33.18). The trigon series is 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, etc. Note that occasionally numbers here also appear in the equilateral or the unequilateral series—for instance, 6, 36.

12. Cf. Theon, Expositio 1.13 (ed. Hiller, p. 27.8-13).

13. That is, 2x3, 3x4, 4x5, 5x6, etc. Again, the numbers in this unequilateral series are seen from two perspectives: first as the sums of addition, then as the products of multiplication. Ficino finds it significant that the equilateral series had resulted in alternating odd and even numbers; cf. Theon, Expositio 1.20 (ed. Hiller, p. 34.1-6).

14. That is, the "long" numbers in the unequilateral series—2, 6, 12, 20, 30, 42, 56, 72, 90, 110, and so on—are always even because they are products of an odd multiplying an even—1x2, 2x3, 3x4, 4x5, 5x6, 6x7, 7x8, 8x9, 9x10, 10x11, and so on. The "oblong" numbers, however, are only two-thirds of them even, namely, when they are products of an even multiplying an even (say 4x6) or of an even multiplying an odd (say 4x7). The remaining one-third are odd, namely, when they are products of an odd multiplying an odd (say 3x7). Hence the distribution of odd and evens in their case is "exceedingly unequal."

15. Theon, Expositio 1.32 and 2.42 (ed. Hiller, pp. 46.14-16, 100.13-14), merely says that 3 is also perfect because it is the first number to have a beginning, middle, and end, and is both a line and a surface; cf. the Theologumena 14.

16. Cf. the Theologumena 2 and 3, which declares that Nicomachus had said that God coincides with the monad. It is a familiar Neoplatonic trope.

17. For the Pythagoreans on 8 as justice, see Macrobius, In Somnium Scipionis 1.5.17-18. Significantly it is not in Theon, Expositio 2.47 (ed. Hiller, pp. 104.20-106.2), or in the Theologumena 72, where we might expect it. Ficino was familiar with Macrobius from the onset of his career.

18. "The odd number" refers, I take it, not to any odd number or even to any one of the three odd numbers just enumerated—3, 7, and 9—but to the 3 alone. The 3 is the prime odd number (and Ficino has so described it in the preceding paragraph), and, as 1-1-1, it can certainly be defined as possessing the bond of itself within, as being circular in a unique way, and as having its extremes agree with its mean. On the other hand, Ficino does not usually think of the 3 as "the principle of the universal order." Indeed, in the opening sentence of chapter 8 below, he will speak of the 1 as the universal cause. Moreover, though the 1 is not strictly speaking an odd number, but the source of all numbers, Ficino will also maintain in that same chapter that Archytas had suggested that the 1 is the Idea of the odd numbers just as the 2 is the Idea of the even, 3 being the first number. The Pythagoreans in general, however, had preferred to think of the 1 as odd and in this special sense the 1 is the archetypal odd, the impar .

The Christian doctrine of the Trinity obviously supports an inclusive interpretation of these apparent alternatives.

1. Cf. Theon, Expositio 1.19 (ed. Hiller, pp. 32.22-33.18).

2. norma is almost certainly intended in the technical sense again of a workman's straight-edged square or rule used for obtaining right angles, i.e., a constant. Ficino is rendering the Greek gnômôn , for which see Theon, Expositio 1.23 (ed. Hiller, pp. 37.11-38.15). Cf. chapter 6, par. iii above.

3. That is, 1, 1+2=3, 3+3=6, 6+4=10, 10+5=15, and so on.

4. That is, 1+3=4, 3+6=9, 6+10=16, 10+15=25—the squares respectively of 2, 3, 4, and 5; and so on. Geometrically such squares are seen in terms of their two (four) constituent right-angled isosceles triangles.

5. Timaeus 31E, 35A, 43D ff., 53B ff., Parmenides 144A, Republic 7.529CD, etc. This does not seem to be a reference to the mathematicals.

6. Plotinus, Enneads 6.6[34].9-15 (which argues that ideal Numbers are even prior to the Forms), also 5.5[32].4-5. I take the Proclus reference here to be to the doctrine of the henads. This was most accessible to Ficino in Proclus's Platonic Theology 3.1-6 (ed. Saffrey and Westerink, 3:5-28) and especially at 3.5; in the Elements of Theology 113-165 (ed. E. R. Dodds, 2d ed. [Oxford, 1965], pp. 100-145); and in the Parmenides Commentary 6.1043.4-1051.33 (ed. Cousin). He may have first encountered the latter in Moerbeke's Latin rendering; see Carlos Steel's introduction to his recent edition, Proclus: Commentaire sur le Parménide de Platon, traduction de Guillaume de Moerbeke , 2 vols. (Louvain and Leiden, 1982-1985), 1:38*-40*.

1. What is the significance here of potius (more) and potissimum (mostly)? The odd are seen as "converting" since they have the 1 as their "hinge" and "center." The even "proceed'' since 2, the first even, is a "falling away" from the 1. This again speaks to the mysterious Platonic elevation of the odd over the even numbers.

2. A commonplace; e.g., Theon, Expositio 1.3 (ed. Hiller, p. 18.3). Note that Ficino is not differentiating here between unitas and unum .

3. Apud Theon, Expositio 1.4—Archytas and Philolaus say the monad is the one—and 1.5 (ed. Hiller, pp. 20.19-20, 22.9-16).

4. Cf. Theon, Expositio 1.5, 2.42 (ed. Hiller, pp. 22.9-16, 100.13-17).

5. See chapter 5, n. 1 above.

6. Cf. Theon, Expositio 1.5 (ed. Hiller, pp. 21.24-22.9).

7. A lost work that Theon cites, Expositio 1.5 (ed. Hiller, p. 22.5-6). Cf. Aristotle's own Metaphysics Alpha 5.985b23 ff. and esp. 986a19-21, and

Physics Gamma 4.203a10 ff. (Kirk-Raven-Schofield, Presocratic Philosophers , nos. 430 and 437, pp. 328-332, 336-337).

8. By the "Pythagoreans" Ficino is probably again thinking specifically either of Archytas, whom Theon in his Expositio 1.5 cites immediately after Aristotle's Pythagorean , or of both Archytas and Philolaus, whom Theon brackets together as using the one and the monad interchangeably (1.4—see n. 3 above). At 2.49 (ed. Hiller, p. 106.10-11) Theon links them as twin authorities on the decad.

9. What is the significance of ab initio here? For 1 as the principle of all numbers, see Theon, Expositio 1.3, 4, 7, 19, 23 (the seed), 31 (the principle of all figures); and 2.44 (but not a number itself) (ed. Hiller, pp. 18.6, 19.21, 24.23, 33.5-7, 37.17-19, 43.4-8, 10-11, 102.4). Cf. chapter 5, n. 1 above.

10. Ficino is contrasting the notion of division as a "tearing apart" ( divellere ) with that of "unfolding" ( explicare ). The first suggests the violence with which Osiris, Attis, and Dionysus were variously sundered; see Wind, Pagan Mysteries , pp. 133-135, 138, 174 ff. The second is part of a triad—enfolded, unfolding, and folding—which signifies the fundamental Neoplatonic triad of rest, emanation, and return ( monê, proodos, epistrophê ).

11. Again, the Platonic reversal of the customary equation of equality and identity with what is even. As the principle of "the same" and as the "indivisible link" in every odd number, the 1's presence mysteriously elevates the odd numbers over the even.

12. That is, the sums of the equilateral addition sequence 1+3, 4+5, 9+7, and so on—which are the same as the products of the multiplication sequence 2x2, 3x3, 4x4, and so on.

13. Equilaterals have "equality and straightness" in that 4, for instance, is the product of 2x2, whereas an unequilateral like 6 is the product of 2x3. As sums, however, the former originates from the 1, the latter from the 2.

14. "Other," I take it, in the sense that their excellence is not "different from" but "more than" just equality, likeness, and straightness.

15. In that the equilateral sequence begins with 1. Again cf. Theon, Expositio 1.23 (ed. Hiller, p. 37.17-18), on unity as the "seed" of all numbers.

16. dum in sua permanet vel geminat unitate is a difficult clause. I take it to mean that since the 1 as seed is enduring, it can remain in its own unity as 1x1 and yet double as 1+1 to 2. We might be tempted to emend to germinat .

17. That is, the seed of an unequilateral like 6 can be thought of as being either of its factors 2 or 3; there is no enduring seed, no 1. Note the emendation. The YMZ reading quadratum is impossible.

18. That is, instead of 2 (the author) multiplying 4 (the instrument), the 2 can multiply itself twice; and similarly with the 3.

19. That is, without the instrumentality of the angels or of the angel who is Neoplatonically equated with Mind, the prime creature.

20. I cannot locate the source of this Pythagorean dictum. Perhaps it is derived from various comments by Aristotle in his account of the Pythagoreans in the Metaphysics 1.5.985b23 ff. (cf. n. 7 above).

21. Cf. chapter 6, n. 18 above.

1. As elsewhere, "compounded" and "procreated" mean "added."

2. That is, 12, an unequilateral, is enclosed on either side by two equilaterals, 16 and 9. In other words, the unequilateral is the proportional mean between the two equilaterals, and 16:12:9 is entirely governed by the ratio of 4:3. Cf. Theon, Expositio 1.16 (ed. Hiller, pp. 28.16-30.7).

3. That is, the next "enclosings" of unequilaterals by equilaterals are: 25:20:16 (governed by the ratio of 5:4), 36:30:25 (governed by the ratio of 6:5), 49:42:36 (governed by the ratio of 7:6), and so on. But Ficino is only interested in the ratios of 4:3, 3:2, and 2:1 because they are contained in the number 12.

4. Epinomis epitome ( Opera , pp. 1529-1530); see Part One, Chapter 1 above. The reference to the epitomes for the Laws is obscure since the issue of proportions is not addressed in them, unless Ficino is thinking of his discussion of twelve(s) in his epitomes for Laws 5, 6, and 12 ( Opera , pp. 1502, 1504-1505, 1522.2 ff.). The more probable reference is to his epitomes for other books of the Republic and especially that for book 10 ( Opera , pp. 1433 ff.).

1. That is, if we think of 8 as a square and not as a cube, then its root is unknown.

2. That is, the diagonal cannot be measured. To square a number is to raise it to a higher power and thus to treat of its potentiality, while to determine the root of such a square is to arrive at its act. Similarly, to square a number is to treat it as a plane, to determine the root of such a square is to treat it as a line.

3. Note the extended metaphor.

1. Ten is not a "long" unequilateral like 6 but an "oblong." It is also of course a trigon. Ficino is skating over some complications here; see Part One, Chapter 2, pp. 55-56 above.

2. The unequilateral sequence, we recall, consists of: 2, 6, 12, 20, 30, 42, 56, 72, and so on. Neither 24 nor 54 is in this series, which consists only of long numbers, i.e., those which, from the perspective of multiplication, are the products of two factors differing only by 1 (as 12 of 3x4 or 72 of 8x9). Rather, they are oblongs, the products that is of two factors differing by more than 1: of 4x6 (or 12x2 or 3x8) and of 6x9 (or 3x18 or 2x27) respectively.

3. Sixty-four is a solid insofar as it is the product of 4x4x4, and 216 is a solid insofar as it is the product of 6x6x6. Ficino is referring throughout to cubes.

1. Cf. Phaedrus 243E-257A, Timaeus 69C-72D, Republic 4.435B-442D, 9.580D ff, 581C, 588C-590C—Plato's major treatments of the soul's tripartition.

2. Meaning, I take it, that if we opt for contemplative, saturnian men as contrasted with active, jovian men. The only difference between these two ideal kinds, as Ficino goes on to declare, is the relationship in them between the understanding ( intelligentia ) and the reason ( ratio ). Both need disciplina , that is, instruction.

3. Notice that air, not fire, predominates in the sanguineous spirit (for which see Ficino's De Vita passim, and especially 1.2). For the ordinary ratios among the simple elements, see Theon, Expositio 2.38 (ed. Hiller, p. 97.4-12) on the fourth quaternary: fire:air is as 1;2, fire:water as 1:3, fire:earth as 1:4, air:water as 2:3, and water:earth as 3:4. The ratios derive from Plato's enigmatic account in the Timaeus at 57D, 58D, 73B, 89C of the various kinds of triangle constituting the elements; cf. chapter 6, n. 11 above.

4. Cf. De Vita 3.12.16-22 (ed. Kaske and Clark).

5. For the notion that heat is a "form" for wetness, again cf. Ficino's De Vita 3.12.20-21, 25-26 (ed. Kaske and Clark) on the dominance of heat in tempering the moisture in our "complexion"; also his Timaeus Commentary 17 ( Opera , p. 144[5]) where fire is compared to form and earth with matter.

6. Opera , pp. 1529-1530. See Part One, Chapter 4, pp. 110-112 and n. 15 above.

7. De Vita 3.5, 6, 11, 21, 22. Cf. Macrobius, In Somnium Scipionis 2.3.14.

8. For these four planets as "the fountains of life," see chapter 3, n. 20 above. Note that Jupiter predominates here, not the Sun.

9. For the astrological theory of elections, see Garin, "Le 'elezioni' e il problema dell'astrologia"; idem, Lo zodiaco , chapter 2. Cf. Ficino's De Vita 3.12.117 ff., 25.9-15 (ed. Kaske and Clark).

10. What does dirigenda mean here?

11. A key term, see Part One, Chapter 3 above.

12. In the twin senses of being instructed and being in control. Undermining discipline are "negligence" and "imprudence," and even just "infelicity."

13. The fatalis ordo is not the thread of personal identity spun by the three Fates as in Hesiod's Theogony 217-222, 904-906, and above all, for Ficino, in Plato's Republic 10.617C ff. Rather it is the great order of Necessity itself as described in the Republic 10.616C and 617B. In his epitome ( Opera , p. 1438), Ficino speaks of the fatum commune , however, and identifies it with providence. He has an important chapter on Fate in his Timaeus Commentary, summa 25 ( Opera , pp. 1670-71). Cf. chapter 15, n. 5 below.

14. Politics 5.12.1316a3-11 (cf. the translation by Benjamin Jowett in the Bollingen Aristotle, 2:2089). See Part One, Chapter 1, n. 19 above.

15. What does Ficino intend by his second alternative? For he proceeds to ignore it.

16. That is, the harmonies of the fourth and the fifth, both of which are contained in the diapason, as we have seen.

1. Presumably Ficino is thinking of the view expounded in the Republic itself.

2. The reference to Pythagoras is obscure, though that to Plato is presumably to the Republic 8.546A ff. The Iamblichus reference may be to the De vita Pythagorica 27.130-131, or possibly to the In Nicomachi Arith. Introd . 82.20-83.18 (which refers to the Republic 8.546). The boethius reference is probably to the De Institutione Arithmetica in general, but we might note that the one allusion to the Republic there is in fact to the passage on the nuptial number and occurs at 2.46 (ed. Friedlein, p. 151.22-25). See Part One, Chapter 1, pp. 32-35 above.

3. This would seem to be implying that the parents on both sides should be odd, notwithstanding the fact that adjacent odd and even numbers constitute the spousal numbers. Perhaps parentes means "progenitors" generally.

4. The diapason is not exactly united with but rather contains the diapente and the diatesseron. See chapter 12, n. 16 above.

5. An obscure reference, probably to another part of this treatise.

6. What is the "praiseworthy" or "excellent" number and what is its "opposite"?

Since the following sentence says the "excellent" number is "fecund," Ficino would seem to be referring either to an "abundant" number—in all likelihood to 1728 as 12 cubed—or to a perfect number—perhaps to 36,000 as the term of the Platonic year. However, he has just declared that 1728 is a fatal number that can produce either good or bad progeny; and in chapters 14 and 15 below he will call it a ''great" but not an "excellent" number!

The "opposite" of the "praiseworthy" number is even less clear, but, given its sterility, it must refer either to a deficient or to an exceedingly imperfect number such as an oblong unequilateral.

7. Notice the traditional distinction between opportunitas for a favorable moment in time, occasio for an unfavorable.

1. Republic 9.587D-588A. Ficino's epitome is silent on 729 and says merely, "Inter haec, casu quodam nescio, quid interserit mathematicum, cuius declarationem ex commentariis in Timaeum accipies opportunius" ( Opera , p. 1427). But the chapters dealing with mathematics in his Timaeus Commentary do not refer to 729 so far as I can determine.

2. "Solid" because the product of 9x9x9, and "circular" because 729 circles back to 9 in that it and 9 both end in 9.

3. In that there are nine celestial spheres: those of the seven planets, that of the fixed stars, and that of the primum mobile.

4. That is, in the course of expounding the myth of Er at 615A ff.; cf. Ficino's epitome ( Opera , pp. 1431-1432).

Ficino finds it significant that Plato had treated of a number ending in 8 in book 8, of a number ending in 9 in book 9, and of a number "procreated" from 10 in book 10. Or at least, he suspects that a Platonist cannot afford to overlook such congruences.

5. Phaedrus 248E ff.; see Ficino's Phaedrus Commentary, summa 25 (ed. Allen, pp. 168-171), with my analysis in Platonism , pp. 177-178. Cf. chapter 15, n. 7 below.

6. This clause is ambiguous: "it" as the subject might also refer to "either square" or possibly to "1728." But Ficino is about to explain Plato's triple mention of 100 in his description of the fatal number.

7. This crux presents difficulties and "only" and "besides" should be omitted. For 728 is oblong in the sense that it is the product, for instance, of 8x91 or 7x104 or 14x52 or 28x26; but it is not long, because it is not the product of two factors differing only by 1. The same is true of 700 as Ficino goes on to explain. Chapter 15, par. i, below refers to "that unequilateral and oblong number, namely 728."

8. The argument of the rest of this paragraph is difficult. In chapter 5 above, Ficino had adduced squares with rational diagonals of 3, 7, 17, and so on. But such values are not part of the equilateral series (4, 9, 16, 25, 49, 64, and so on) unless they are themselves squared. Here he must be thinking therefore, not of rational diagonals as such, but rather of their "powers" or squares—that is, of 9, 49, 289, and so on. Thus he interprets Plato's "twin" 100's to mean a hundred squares (including such diagonal powers) and a hundred cubes. See Part One, Chapter 2, pp. 76-79 above.

9. I.e., to 10,000. The myriad is the "numberless crowd," given that murias in Greek means both "ten thousand" and more generally "a countless number."

10. I.e., up to the myriad. Ficino is not saying that the powers of certain rational diagonals—powers such as 9, 49, 289, and so on—are a myriad, but merely that they are included in it. Indeed, in chapter 15, par. v, he will hint that the number of such powers so included is 100.

11. Meaning, presumably, if you cube existing cubes, for instance, 27x27.

12. I take this to mean that, while the limit for squares (including the diagonal powers) is 100 ² , the limit for cubes is 100 ³ the million not the myriad. But the operative root for both remains the 100 (which in turn has as its own root the 10).

13. That is, subsequent to the eighth celestial sphere of the fixed stars.

14. I doubt Ficino has the specific ratio of 1000:28 (i.e., 250:7) in mind.

15. That is, to the six other planets. The specific ratio of 700:28 (i.e., 25:1) is again probably not what Ficino intended.

16. Ficino is thinking of the six higher planets as a group. What does he mean by "a similar proportion" here between the elemental wetness and the Moon, between the Moon and the planets, and between the planets and the firmament? Clearly he no longer has the musical intervals of the Epinomis in mind as in chapter 12 above.

17. Ficino must mean here both all even numbers and all the numbers in the equilateral series of 4, 9, 16, 25, and so on (half of which are odd)! He cannot mean all even numbers but especially the equilateral numbers that are even, since he goes on to link the unequilateral series, none of which are odd, with the odd numbers.

18. That is, all odd numbers (and not just the odd numbers in the equilateral series) plus the numbers in the unequilateral series of 6, 12, 20, 30, and so on (all of which are even)! The point seems to be to contrast generally all even with all odd numbers, and then more specifically all the numbers (odd and even) in the equilateral series with all those in the unequilateral (all of which are even). He does not intend to reconcile the two categories.

In the next paragraph, Ficino will distribute the plane and solid, lateral and diagonal numbers among the planets.

19. "Oblongs" mean, we recall, those numbers having factors differing by more than 1, e.g., 15=3x5. Ficino observes below that both odd and even numbers can be predicated of the planets, depending on the point of view.

20. He has already just assigned the equilateral numbers to the firmament, and the unequilaterals (i.e., the longs) to the planets and the elements. Now he is subdividing the latter category and designating as oblongs the three planets and the two elements that are subject to the most motion.

21. The "great spheres" of the planets as contrasted with the lesser spheres of the elements.

22. That is, if we are comparing the planets with the elements, then we can think of all of them as even, but within the planets as a category evenness is associated with the Sun, Jupiter, and Venus and oddness with the Moon, Mercury, and Mars. Similarly, within the elements as a category evenness is associated with the upper aethereal air and with the middle air, whereas oddness is associated with fire and with water. Interestingly, Ficino avoids mentioning both Saturn and Earth/earth in these comparative distributions that are now privileging the even.

23. Ficino now proceeds to subdivide the planets in terms of plane and solid and to privilege the solid.

24. In other words, the Moon, Mercury, Venus, and Mars are subordinate planets that "refer" to, in the sense of "answer" to, the solidity, the "fullness" of the other three. See n. 28 below.

25. Cratylus 396AB: "Wherefore we are right in calling Jupiter Zena and Dia, which are one name, although divided, meaning the god through whom all creatures always have life" (" di' hon zên aei pasi tois zôsin huparchei "—396B1-2). Plato derives Cronos from Koros as signifying "the pure and garnished mind" (" to katharon autou kai akêraton tou nou "—396B6-7). Cf. Ficino's Cratylus epitome ( Opera , p. 1311).

26. Laws 4.713A: "the god who is the master of rational man."

27. The "ingenious gift" means the powers that Saturn bestows on our intellect, on our ingenium .

28. Note that the "solid" Sun has two ministering "plane" planets, while Jupiter and Saturn each have only one. The link between Jupiter and Venus is especially significant for Ficino given Plotinus's suggestion that "priests and

theologians" have identified the higher Venus not only with Juno but with Zeus. Venus can thus signify the World-Soul; cf. Enneads 3.5.2.15-20, 3.5.8.20-24, 5.8.13.16-18. See my Platonism , pp. 130-132.

29. That is, the Moon is the diagonal to Venus's side since she is "bearing" (i.e., duplicating) the "power" of Venus's side.

30. The importance of such metaphors is stressed in the Timaeus at 27CD, 29D, and in the Phaedrus at 246A, 257A.

31. De Vita 3.23-25.

1. That is, having focused on the last three digits in 1728.

2. That is, this second or diagonal 100 is the number "of equal length" which multiplies the number sacred to Pallas, the 7, to give us the 700 in the great number 1728. In the parentheses I take Ficino to be saying that this 100 can be viewed either as an integer ( pariter ) or as the product of 10 ² ( planum ).

3. In short, Ficino is extracting the 100 thrice: as the square root of 10,000 (the myriad being the hundredth square); as 10 ² ; and as the cube root of 1,000,000 (the million being the hundredth cube). The passage is difficult. Ficino will be arguing almost immediately that Plato also "secretly" intends 10,000 here.

4. That is, the three as triply present: in the three 100's; in the threesome of 100, 1000, and 10,000; and in the three terms in 1728 (i.e., 1000, 700, and 28).

5. For this Platonic allegorization of the Fates see Republic 10.617C and Ficino's epitome ( Opera , pp. 1434-35); see too his epitome for Laws 12 ( Opera , p. 1525), and his De Vita 2.20.57-62 (ed. Kaske and Clark). Cf. chapter 12, n. 13 above.

6. Republic 10.615AB. Cf. Ficino's epitome: "si ad centum usque vixissent annos, quo termino vita hominum quodammodo designatur" ( Opera , p. 1432).

7. Phaedrus 248E-249B. Cf. Ficino's Phaedrus Commentary, summa 25 (ed. Allen, p. 169), and his Republic 10 epitome ( Opera , p. 1432). See my Platonism , pp. 177-179. Cf. chapter 14, n. 5 above.

8. The myriad has "equal" dignity as 100x100, but "unequal" dignity as 10x1000. The two references are I believe to the "secret" presence of 10,000 here in the Republic 8 at 546C, and again in the Phaedrus at 248E; cf. n. 21 below. Ficino's Phaedrus Commentary, summa 25 (ed. Allen, pp. 168-170) declares that 10,000 signifies the "slowness" with which men return to their native land.

9. That is, if we cube every number from 1 to 100, the hundredth in the resulting cubes is the million.

10. Citing Plato's phrase at 546C6, " hekaton de kubôn triados ."

11. In the earlier instance 10 is taken as the line, in the later instance 100—with the resulting adjustments. Ficino sees Plato concentrating upon

100 as the basic number of time: it is the marker of the centuries, of both the planes and the depths, as it were, of time. Cf. his Republic 10 epitome ( Opera , p. 1432).

12. Citing the phrase at 546C3, " tên men isên isakis, hekaton (var. hekaston ) tosautakis ."

13. I.e., through the territory of the "innumerable planes" and powers below 10,000 (see n. 3 above) or possibly between 10,000 and a million. The diagonal numbers, we recall, are often thought of in terms of their "powers" and thus as planes.

14. This famous phrase is repeated in chapter 16.16 below.

15. The referent is not clear, but I take haec omnia to be referring to the "planes and solids." Cf. Timaeus 32AB, 53C-56A and its description (based on the assumption that every rectilinear surface is made up of triangles) of the mix of the five regular solid figures that underlie both celestial and terrestrial matter.

16. Again the referent is not clear—the quorum could be referring to the preceding haec omnia (and thus, if I am correct there, to the "planes and solids"). However, I take it to be referring directly to "the celestials and the elements" because of the idea of motion. In either case, Ficino's meaning is obvious: plane and solid numbers can be said to underlie celestials and terrestrials and to endow them with their powers and motions.

17. In the sense of "began" or more literally in the sense of "drew out of"? Ficino may be playing on the subtle distinction between producere and the deducere of the next line.

18. Six is the first perfect number, we recall, because it is the first to equal the sum of its factors of 3, 2, and 1.

19. That is, since 2 and 8 are the last two digits in the fatal number of 1728, 28 is the "terminus," meaning the end and limit of that number. Just as 12 (as 2x6) was its "entrance," so is 28 its "exit."

20. There is no one "great" number: "great" is used of 1728 at the beginning of this paragraph, of 10,000 at the end.

21. The rest of this paragraph is difficult. The "innumerable number" has been equated elsewhere with the 10,000, and Ficino seems to be saying that it (as well as the 100) is secretly presented here by Plato, and presented in three guises (3 being the first and "most sacred" of all numbers): as 100 ² ; as the number containing 100 diagonal and therefore 100 lateral powers; and as the principal factor, along with the 100, of a million. Cf. n. 8 above.

22. That is, he presents 10,000 as 100 ² (i.e., in terms of its "equal dignity").

23. The formula for "arranging" and "increasing" these numbers has been given in chapter 5 above.

24. meaning, I take it, the diagonal powers (squares) that we derive from the lateral powers (squares) as 7 ² from 5 ² +5 ² -1; that is, as chapter 5 has already argued, the creation of larger square numbers from smaller.

25. The 10,000 as 100 ² is multiplied by 100 again to produce the cube, the million. The square is therefore present in the cube and the million is the hundredth, the "amplest" cube. See n. 9 above.

26. Ficino seems to be arguing that all compounded, all sublunar things cannot outlast 10,000 years.

27. That is, individual things, given the transitoriness of their constituent triangles, have their own spans (which are much smaller than 10,000). Cf. Timaeus 89C (on individuals and diseases).

28. The "certain parts" of "such a great number" I take to be referring to the parts of 10,000, namely to 10, 100, and 1000 as its factors, but Ficino may be thinking of 1728 and its "parts," namely of 1000, 700, and 28.

1. Statesman 309A ff., 309E-311A; Laws 4.721A.ff., 6.722D-773E, 775B-E, 783D-785B; cf. 5.735B ff.

2. A crux: aequalissima could qualify the distant preceding ingenia or the immediately preceding progenies or the succeeding utraque vero ingenia . The sense demands, I believe, the latter and I have punctuated and translated accordingly. The two different dispositions should each be the "most tempered" (cf. a few lines below where the diapason is likewise described as "most equal," meaning "most tempered") and the most "elect" in their class, but expressly not ''most equal" to each other. In chapter 17 below, at the end of par. vii, he will call the divine class of perfect numbers "equal and tempered," since it "depends on, and stands firm in, its parts and powers."

3. The "higher wetness" refers here to air, which is warm and moist, the "lower wetness" to water, which is cold and moist, fire being hot and dry, earth cold and dry. Cf. Ficino's Timaeus Commentary 17 ( Opera , p. 144[5].1), which defines humor as ignis terraeque conciliator and then subdivides it into igneus, terreus , and aer purus, humor terreus being ordinary water and humor igneus being aether Platonically conceived as intermediate between the pure air and the pure fire (see the Epinomis 981C, 984B-E).

4. Cf. chapter 3, n. 7 above.

5. I have introduced the semicolon after imparibus to make it clear that velut in quadratis numeris should not govern inaequales autem ex paribus . For Ficino simply means, I take it, that even habits are like the square numbers (i.e., 4, 9, 16, 25, and so on) generated in the equilateral addition series from the odd numbers, whereas odd habits are like the non-square numbers generated in the unequilateral series from the even numbers. He cannot mean that odd habits are like the odd sums in the equilateral series (where they could be said to be generated from an even number only in that any alternate sum in the series is necessarily even—1+3=4, 4+5=9, 9+7=16, 16+9=25, and so on—and that the next odd number is added to it). See Part One, Chapter 3, pp. 85-86 above.

6. Note that these are the life-giving planets; cf. chapter 3, n. 20 above.

7. Ficino may be referring not to Plato's portrait of a republic but to the Republic itself at 5.458E ff., 459E, 460E-461B, or 8.546A ff.

8. Laws 6.771E ff., 772D-773D, 775C-E (and esp. 773A-D).

9. Laws 6.773CD.

10. Since 35 itself must be the oblong (as 5x7)—see chapter 6, par. i above—what is the long that Plato "explicitly" intends here? I believe Ficino must be thinking of 30 (which as 5x6 is a long), because, as the opening sentence of this paragraph has already declared (following the Laws 6.772DE), a man should enter upon marriage between 25 and 35, the arithmetic mean of which is 30. Furthermore, as the next paragraph is about to declare (following the Republic 5.460E), a man's time for begetting lasts from 30 (his prime) to 55, a period of 25 years (30 is also the mean age for a woman to give birth). Perhaps we should simply emend the text to read Denique ubi inducit 30 et 35 .

11. That is, Ficino sees Plato intending by his introduction of 35 to suggest not only 30 but also 36. For 36 is the nearest circular to 35 and also the nearest power or square to it in the equilateral series; 36 is thus the "term" of 35.

12. Republic 5.454-463 (and esp. 460E); cf. Laws 6.772D.

1. This is actually the Porphyrian order, since the strictly Platonic order, as derived from the Timaeus 38C-E, reverses the positions of Mercury and Venus, though Ficino probably thought of them as identical. The principal contrasting order for him is the Chaldaean-Ptolemaic: Saturn, Jupiter, Mars, Sun, Venus, Mercury, Moon, an order he usually adheres to in nonastronomical contexts given its well-nigh universal acceptance during the Middle Ages; cf. Ficino's Timaeus Commentary 35 ( Opera , p. 1461). See my Platonism , p. 118, n. 17, with further details.

2. In the following paragraph Ficino mentions "the rest" of the perfect numbers and this suggests he had envisaged those beyond 8128. See Part One, Chapter 2, nn. 20, 22 above.

3. Ficino is intrigued by the fact that the last digits in the sequence of the first four perfect numbers—6, 28, 496, 8128—alternate between 6 and 8 and supposes this true for higher perfect numbers. Again see Part One, Chapter 2, nn. 21, 22 above.

4. That is, in terms of its being a square or cube root.

5. Book 3 of the De Vita in particular is concerned with the problem of how to "capture" the astrologically auspicious moment, the moment best suited to our character, our ingenium , our inner and outer daemons and their powers. In particular see 3.23.1-17 (ed. Kaske and Clark).

6. Cf. De Vita 3.5 and 3.19.54-58 ff. (ed. Kaske and Clark).

7. The subject of quando nobiscum ita consonat is unclear. It could mean: "when Jupiter accords with us thus" or more probably "when the whole harmony of all seven planets accords with us thus" (there being six intervals between them). "Celestials" always refers to the planets, not to the stars in the firmament.

8. Cf. Ficino's epitome for Laws 4 ( Opera , p. 1498).

9. Cf. De Vita 3.22.33-44 (ed. Kaske and Clark), where Jupiter is described as "the temperer" of Saturn.

10. Cf. De Vita 3.4.66-68 (ed. Kaske and Clark), where the sextile aspect is defined as being the time when two planets are two signs away from each other, the trine aspect when they are four.

11. One of the senses of affectio is "planetary aspect" and Ficino is playing off this.

12. That is, the Moon serves to temper the Sun as Jupiter tempers all things. I take agit here to imply that the Moon "acts the part" of Jupiter.

13. Meaning at the time of conjunction? Cf. De Vita 3.6.102-106, 18.89-91 (ed. Kaske and Clark).

14. Cf. De Vita 3.6.115-123 (ed. Kaske and Clark).

15. For Venus as a lesser Jupiter, again cf. Plotinus, Enneads 3.5.8 and 5.8.13. Notice that Ficino is once more focusing on the life-giving planets.

16. In the last paragraph of chapter 14 above, Ficino had already described Mercury as moving with "the ingenious gift" of Saturn, or accompanying or executing it. Cf. his letter to Filippo Carducci of 14 November 1492:

Mercurio Saturnum insuper addidi sive comitem sive ducem. Lego hodie in X de Republica Mercurium Saturnumque colore, id est luce, ita consimiles esse ut alter quidem ad sapientiam exhortetur, alter vero, Deo videlicet altius aspirante, perducat. Dei quidem imaginem esse Solem volunt. Deus ipse est auctor sapientiae primus. Sapientiae significatores, Mercurius atque Saturnus, imaginis divinae comites minime omnium a Sole discedunt, dum videlicet et Mercurius sub Solis splendore ferme semper incedit, et Saturnus ab eclyptica Solis via minime omnium praevaricari videtur. Hos astronomi natura quadam similes esse putant Mercuriumque aedibus et finibus et aspectu Saturni gaudere. Hic (ut opinor) efficitur ut ferme omnes qui a Mercurio suum iter professionemque exordiuntur solum desinant in Saturnum. ( Opera , p. 948.3)

Cf. also his De Vita 1.4.1-9 (ed. Kaske and Clark).

17. Compare, for instance, Ficino's epitome for Laws 4 ( Opera , p. 1498) on "the reign of Saturn," and his De Vita 3.22.45 ff. (ed. Kaske and Clark).

18. in quos fines seculorum pervenerunt may also imply that the ends of the ages were perfected in and by the coming of such divine men. Ficino probably has in mind Plato's references to the "shepherds" in the Statesman 's great myth at 271D ff. and 275B ff.; cf. his epitome for that dialogue ( Opera , p. 1296), and an unattached chapter of his Philebus Commentary (ed. Allen, p. 435).

19. Vergil, Eclogues 4.4-7 (with the omission of line 6). Ficino occasionally quoted, paraphrased, or adapted this text; see, for instance, his letter of 6 January 1482 (n.s.) to Duke Federico of Urbino in the seventh book of his Epistulae : "Quum etiam Sibylla Cumaea tempore eadem descripsisse videtur, quibus magnus ab integro seculorum nasceretur ordo ac floreret virgo novaque progenies ex alto demitteretur" ( Opera , p. 852.2).

20. Wisdom of Solomon 11.20[21]. See Appendix 3 below.

21. Cf. the Expositio prefacing the De Numero Fatali : "sermonem vero hominibus inexplicabilem merito Musis attribuit." It is "inexplicable" because "inextricable."